About This Page
List of Problems
Resources
Contact
List of Open Problems
- The Cuntz Splice for Leavitt path algebras. If E is a graph, the operation of the Cuntz splice attaches a
portion to the graph that changes the sign of det (I–At), where A is the vertex matrix of E. Here is an example: In the following graph, we attach the Cuntz
Splice at the starred vertex, and label the adjoined vertices and edges.

The Cuntz splice is important in the classification of C*-algebras of finite graphs. As a special case of the construction, we can consider the graph with a single vertex and two edges, which we denote E2, and the graph formed by performing a Cuntz splice to it, denoted E2–.
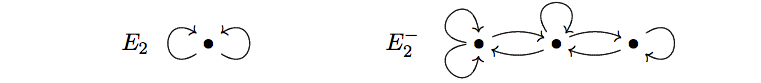
In [Rør95] Rørdam showed that C*(E2) is isomorphic to C*(E2–). It automatically follows from this that if E is any finite graph whose associated algebra is simple and purely infinite, and if F is the graph formed by performing the Cuntz splice at any vertex of F, then C*(E) is Morita equivalent to C*(F). (More generally, Eilers, Ruiz, and Sørensen have shown in a forthcoming preprint, that if E is any graph with a finite number of vertices and if F is the graph formed by performing the Cuntz splice at any vertex of E that is the base point of two distinct cycles, then C*(E) is Morita equivalent to C*(F).)
The classification for Leavitt path algebras of finite graphs has been hindered by the lack of analogous results concerning the Cuntz splice. In particular, the following are important open problems.
Question: Let E be a graph whose associated algebra is simple and purely infinite, and let K be any field. If F is the graph formed by performing the Cuntz splice to any vertex of E, then is LK (E) Morita equivalent to LK (F)?
The answer to the above question is the last remaining piece in the classification of unital Leavitt path algebras. See [RT13, Section 8] for a discussion of these issues.
Question: If K is any field, then are LK(E2) and LK(E2–) isomorphic as rings? (Note: Sometimes in the notation, the field K is suppressed and one writes L2 and L2– in place of LK(E2) and LK(E2–), respectively. The question is then often stated as: Are L2 and L2– isomorphic?)
Comment: Since the algebraic K0-groups of LK(E2) and LK(E2–) are both zero, these algebras will be Morita equivalent if and only if they are isomorphic. In addition, we mention that all algebraic K-groups of these two algebras are zero, so the K-groups cannot be used to distinguish between the two.
Comment: One can verify that the homogeneous zero components of LK(E2) and LK(E2–) have different K0-groups and hence are not isomorphic. Thus there does not exist a graded isomorphism from LK(E2) onto LK(E2–).
Comment: Unlike in the C*-algebra case, an affirmative answer to the second question does not immediately imply an affirmative answer to the first. For a discussion of what extra properties are needed, see [ALPS11, Section 2], particularly "The Hypothesis" listed there.
References
[ALPS11] G. Abrams, A. Louly, E. Pardo, and C. Smith, Flow invariants in the classification of Leavitt path algebras, J. Algebra 333 (2011), 202--231.
[Rør95] M. Rørdam, Classification of Cuntz-Krieger algebras, K-Theory 9 (1995), no. 1, 31--58.
[RT13] E. Ruiz and M. Tomforde, Classification of unital simple Leavitt path algebras of infinite graphs, J. Algebra 384 (2013), 45--83.
- K-groups of unital Leavitt path algebras. In [RT13, Example 11.2] an example was given of graphs E and F that each have associated algebras that are unital, simple, purely infinite, and have the property that
K0 (Lℚ(E)) ≅ K0 (Lℚ(F)) and K1 (Lℚ(E)) ≅ K1 (Lℚ(F)), but
K2 (Lℚ(E)) is not isomorphic to K2 (Lℚ(F)). (Here, ℚ denotes the field of rational numbers.)
Question: For a given field K and any natural number N, do there exist graphs E and F, each with a finite number of vertices, an infinite number of edges, and associated algebras that are simple and purely infinite, such that Ki (LK(E)) ≅ Ki (LK(F)) for all 1 ≤ i ≤ N-1, but KN (LK(E)) is not isomorphic to KN (LK(F))?
It follows from [RT13, Theorem 7.1] that such a field K must necessarily be a field with free quotients, as defined in [RT13, Section 6].
References
[RT13] E. Ruiz and M. Tomforde, Classification of unital simple Leavitt path algebras of infinite graphs, J. Algebra 384 (2013), 45--83.
- Twisted k-graph algebras. In [KPS12] and [KPS11] it was described how a
Τ-valued 2-cocycle c on a k-graph Λ can be incorporated into the relations defining the associated C*-algebra to
obtain a twisted k-graph C*-algebra C*(Λ, c). (Here Τ denotes the unit circle consisting of complex numbers of modulus one.) It was shown in [KPS13] that if C*(Λ) is a Kirchberg algebra,
then C*(Λ, c) ≅ C*(Λ) for any 2-cocycle c. In [ACaHR13] the authors showed that for a k-graph Λ
and a ring R one can define a "higher-rank Leavitt path algebra" KPR(Λ), which they call a Kumjian-Pask algebra over R.
For a 2-cycle c it is possible to mimic the definition of a twisted k-graph C*-algebra to define a "twisted Kumjian-Pask algebra" KPR(Λ,c).
This raises the following question.
Question: Let C denote the field of complex numbers. Does there exist a 2-graph Λ and a Τ-valued 2-cocycle c on Λ such that C*(Λ) is a Kirchberg algebra, and KPC(Λ) is not isomorphic to KPC(Λ, c)?
References
[ACaHR13] G. Aranda Pino, J. Clark, A. an Huef, and I. Raeburn, Kumjian-Pask algebras of higher-rank graphs, Trans. Amer. Math. Soc. 365 (2013), 3613--3641.
[KPS11] A. Kumjian, D. Pask and A. Sims, On twisted higher-rank graph C*-algebras, preprint 2011.
[KPS12] A. Kumjian, D. Pask, and A. Sims, Homology for higher-rank graphs and twisted C*-algebras, J. Funct. Anal. 263 (2012), 1539--1574.
[KPS13] A. Kumjian, D. Pask, and A. Sims, On the K-theory of twisted higher-rank-graph C*-algebras, J. Math. Anal. Appl. 401 (2013), 104--113.
- Moves on Graphs. If E and F are graphs with a finite number of vertices, it follows from results of
[CK80], [Rør95], and [Sør12] that C*(E) is Morita equivalent to C*(F) if and only if the graph E may be transformed into the graph F using
the following five moves and their inverses: (S) Source Removal, (O) Outsplitting, (I) Insplitting, (R) Reduction, and (C) Cuntz Splice.
Question: Is there a set of graph moves that generates Morita equivalence for all graph C*-algebras? In other words, is there a set of graph moves such that if E and F are (possibly infinite) graphs, then C*(E) is Morita equivalent to C*(F) if and only if E may be transformed into F using these moves?
Question: Is there a set of graph moves that generates isomorphism for graph C*-algebras? In other words, is there a set of moves such that if E and F are (possibly infinite) graphs, then C*(E) is isomorphic to C*(F) if and only if E may be transformed into F using these moves? (An answer to this question would be interesting even under the hypotheses that E and F are finite graphs whose associated C*-algebras are simple.)
With regards to the first question, a starting point is to consider the graph
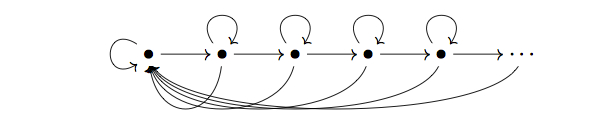
The C*-algebra of this graph is nonunital, simple, and purely infinite. By computing the K-theory of this C*-algebra, we see that it has the same K-groups as the Cuntz algebra O∞, and thus by the Kirchberg-Phillips classification theorem, this C*-algebra is Morita equivalent to O∞. Since O∞ is the C*-algebra of the graph

an answer to the first question would require one to find a move that would change the first graph into the second. To date, no one has been able to show that the C*-algebras of these two graphs are Morita equivalent without using the Kirchberg-Phillips classification theorem. In addition, it is unknown if the Leavitt path algebras of these two graphs are Morita equivalent.
References
[CK80] J. Cuntz and W. Krieger, A class of C*-algebras and topological Markov chains, Invent. Math. 56 (1980), 251--268.
[Rør95] M. Rørdam, Classification of Cuntz-Krieger algebras, K-Theory 9 (1995), no. 1, 31--58.
[Sør12] A.P.W. Sørensen, Geometric classification of simple graph algebras, preprint 2012.
- Dependence of Isomorphism Class on the Field.
Question: Do there exist graphs E and F and fields K and K' such that LK (E) ≅ LK (F), but LK' (E) is not isomorphic to LK' (F)? Likewise, do there exist graphs E and F and a field K such that LK (E) ≅ LK (F), but Lℤ(E) is not isomorphic to Lℤ (F), where ℤ denotes the ring of integers?
See [Tom11] for the definition of and basic results for Leavitt path algebras over rings.
References
[Tom11] M. Tomforde, Leavitt path algebras with coefficients in a commutative ring, J. Pure Appl. Algebra 215 (2011), 471--484.
- The Isomorphism and Morita Equivalence Conjectures. These conjectures
were first posed by Abrams and Tomforde in [AT11].
The Isomorphism Conjecture: Let ℂ denote the field of complex numbers. If E and F are graphs and if Lℂ(E) and Lℂ(F) are isomorphic as rings, then are C*(E) and C*(F) isomorphic as C*-algebras?
The Morita Equivalence Conjecture: Let ℂ denote the field of complex numbers. If E and F are graphs and if Lℂ(E) and Lℂ(F) are Morita equivalent as rings, then are C*(E) and C*(F) strongly Morita equivalent as C*-algebras?
See [AT11] for the first appearance of these conjectures. Also see [AT11] and [RT13] for partial progress, and lists of classes of graphs where the conjectures are known to hold.
References
[AT11] G. Abrams and M. Tomforde, Isomorphism and Morita equivalence of graph algebras, Trans. Amer. Math. Soc. 363 (2011), 3733--3767.
[RT13] E. Ruiz and M. Tomforde, Ideal-related K-theory for Leavitt path algebras and graph C*-algebras, Indiana Univ. Math J., to appear.
- Continuous Orbit Equivalence. If E is a graph,
the subalgebra D(E) is defined to be the closure of span { Sα Sα* : α is a finite path }.
One can show that if the graph E satisfies Condition (L), then D(E) is a MASA of C*(E).
Given a graph E, we let ΣE denote the one-sided shift space consisting of one-sided infinite paths in E together with
the canonical shift map.
In [Mat10, Theorem 1], Matsumoto proves that if E and F finite graphs with no sinks and whose associated C*-algebras are simple, then
ΣE and ΣF are continuously orbit equivalent if and only if there an isomorphism
φ : C*(E) --> C*(F) with φ (D(E)) = D(F). (The definition of "continuously orbit equivalent" can be found in
[Mat10].)
This raises the following questions.
Question: If E and F are graphs and C*(E) ≅ C*(F), then is there an isomorphism φ : C*(E) --> C*(F) with φ (D(E)) = D(F)?
Question: If E and F are graphs and C*(E) is strongly Morita Equivalent to C*(F), then is there a Morita equivalence between C*(E) and C*(F) that preserves D(E) and D(F)?
In [Mat13, Theorem 4.3] Matsumoto has proven that if E and F are finite graphs with no sinks and whose associated C*-algebras are simple, and if the sign of det (I–At) is equal to the sign of det (I–Bt) (where A and B are the vertex matrices of E and F, respectively), then C*(E) is isomorphic to C*(F) if and only if ΣE and ΣF are continuously orbit equivalent. In [Mat13, Section 6] Matsumoto states that there are no known examples of one-sided shifts ΣE and ΣF that are continuously orbit equivalent and with sign of det (I–At) not equal to the sign of det (I–Bt). This has led Matsumoto to make the following conjecture.
Matsumoto's Conjecture: If E is a graph with one-sided shift ΣE and vertex matrix A, then det (I–At) is an invariant of the continuous orbit equivalence class of ΣE.
Matsumoto points out in [Mat13, Section 6] that if this conjecture is true, the triple (K0 (C*(E)), [1]0, det (I–At)) would be a complete invariant for the continuous orbit equivalence class of the one-sided shift ΣE. This would imply that two one-sided topological Markov shifts ΣE and ΣF are continuously orbit equivalent if and only if the graph C*-algebras C*(E) and C*(F) are isomorphic and det (I–At) = det (I–Bt).
References
[Mat10] K. Matsumoto, Orbit equivalence of topological Markov shifts and Cuntz-Krieger algebras, Pacific J. Math. 246 (2010), 199--225.
[Mat13] K. Matsumoto, Classification of Cuntz-Krieger algebras by orbit equivalence of topological Markov shifts, Proc. Amer. Math. Soc. 141 (2013), 2329--2342.
- Analogues of O2 ⊗ O2 ≅ O2.
A famous and important theorem of Elliott (which was exposited by Rørdam in [Rør95]) states that O2 ⊗ O2 ≅ O2.
It is natural to ask if an analogue of this result holds for the Leavitt algebra with two generators. If K is a field, and L2 denotes the Leavitt algebra with two generators over K (i.e.,
the Leavitt path algebra of the graph with one vertex and two edges), then Ara and Cortiñas showed in [AC12] that L2 ⊗ L2 and L2
are not isomorphic, and indeed not even Morita equivalent. However, one can still ask the following question.
Question: Is L2 ⊗ L2 isomorphic to a subalgebra of L2?
Equivalently, one may ask if there exists an injective homomorphism φ : L2 ⊗ L2 --> L2, and since L2 ⊗ L2 is simple it suffices to produce a nonzero homomorphism φ : L2 ⊗ L2 --> L2. Moreover, since eL2e is isomorphic to L2 for any nonzero idempotent e in L2, the existence of a nonzero homomorphism from L2 ⊗ L2 into L2 implies the existence of a unital injective homomorphism from L2 ⊗ L2 into L2.
References
[AC12] P. Ara and G. Cortiñas, Tensor products of Leavitt path algebras, Centre de Recerca Matematica, Preprint 1042, 2011.
[Rør95] M. Rørdam, A short proof of Elliott's theorem: O2 ⊗ O2 ≅ O2. C. R. Math. Rep. Acad. Sci. Canada 16 (1994), 31--36.
- Lp-versions of the Cuntz algebras and UHF algebras.
Chris Phillips has defined Lp-versions of the Cuntz algebras for p ∈ [1,∞], which are denoted Odp. Definitions and basic facts for these objects can be found in
his paper [Phi12] as well as the slides from his talk at the BIRS Workshop on Graph Algebras.
Phillips has created a long list of open problems, which we make available in PDF form here:
Chris Phillips' list of problems on Lp-versions of the Cuntz algebras and UHF algebras
We highlight one problem from this list (see Problem 5.3 in the PDF), which is particularly intriguing.
Question: For which values of p ∈ [1,∞] is it true that O2p ⊗p O2p is isomorphic to O2p?
References
[Phi12] N.C. Phillips, Analogs of Cuntz algebras on Lp-spaces, preprint (2013).
- One-sided and two-sided shift spaces.
If E is a finite graph with no sinks or sources, we let ΣE denote the one-sided shift space consisting of one-sided infinite
paths in E, and we let XE denote the two-sided shift space consisting of two-sided bi-infinite
paths in E. It is well known that for irreducible graphs, the Morita equivalence class of C*(E) is closely related to flow equivalence class of
XE (see [Rør95]). In particular, if E and F are finite graphs with no sinks whose associated algebras are simple, then
XE is flow equivalent to XF if and only if C*(E) is Morita equivalent to C*(F) and the sign of
det (I–At) is equal to the sign of det (I–Bt) (where A and B are the vertex
matrices of E and F, respectively). One may ask how other dynamical properties of ΣE and XE
are related to the isomorphism class and Morita equivalence class of C*(E).
Question: Let E and F be finite graphs with no sinks or sources. It is known that if the two-sided shifts XE and XF are conjugate, then there is a gauge-invariant Morita equivalence between C*(E) and C*(F). Can a converse, or partial converse, to this result be obtained? In other words, if there is a gauge-invariant Morita equivalence between C*(E) and C*(F), what additional hypotheses are needed to ensure that XE and XF are conjugate?
Question: Let E and F be finite graphs with no sinks. It is known that if the one-sided shifts ΣE and ΣF are conjugate, then there is a gauge-invariant isomorphism between C*(E) and C*(F). Can a converse, or partial converse, to this result be obtained? In other words, if there is a gauge-invariant isomorphism between C*(E) and C*(F), what additional hypotheses are needed to ensure that ΣE and ΣF are conjugate?
Question: Let E and F be finite graphs with no sinks. Is there a notion of flow equivalence for the one-sided shift ΣE? If not, can one be developed? Is the flow equivalence class of ΣE related to the isomorphism class or the Morita equivalence class of C*(E)?
Note: This problem and the questions it asks are related to Problem 13 below.
References
[CK80] J. Cuntz and W. Krieger, A class of C*-algebras and topological Markov chains, Invent. Math. 56 (1980), 251--268.
[Rør95] M. Rørdam, Classification of Cuntz-Krieger algebras, K-Theory 9 (1995), no. 1, 31--58.
- Separated Graph Algebras.
In [AG11] and [AG12] Ara and Goodearl introduced separated Leavitt path algebras (generalizing the Leavitt algebras L(m,n)), and they also introduced their
C*-algebra counterparts. If (E,C) is a separated graph, we let M(E,C) denote the abelian monoid with generators
{av : v ∈ E0} satisfying the relations av = Σe ∈ X ar(e)
for all v ∈ E0 and all X ∈ Cv. It was shown in [AG12, Theorem 4.3] that there is a natural map
M(E,C) --> V(L(E,C)) sending av to [v] ∈ V(L(E,C)), where V(L(E,C)) is the abelian monoid
of Murray-von Neumann equivalence classes of projections in matrices over L(E,C). If we let V(C*(E,C)) denote the abelian monoid
of Murray-von Neumann equivalence classes of projections in matrices over C*(E,C), there is a similar natural map M(E,C) --> V(C*(E,C)) sending av to [v] ∈ V(C*(E,C)).
Question: Is the natural map M(E,C) --> V(C*(E,C)) an isomorphism? (This is equivalent to asking if the natural map V(L(E,C)) --> V(C*(E,C)) is an isomorphism.)
The result is certainly true for non-separated graphs [AMP07, Theorem 7.1]. In addition, if the answer to this question is positive, it would follow, as in [AG12, Corollary 4.5], that every conical abelian monoid is isomorphic to V(C*(E,C)) for some finitely separated graph (E,C). If the answer is negative, one would still like to know whether this map is always injective.
References
[AG11] P. Ara and K.R. Goodearl, C*-algebras of separated graphs, J. Funct. Anal. 261 (2011), 2540--2568.
[AG12] P. Ara and K.R. Goodearl, Leavitt path algebras of separated graphs, J. Reine Angew. Math. 669 (2012), 165--224.
[AMP07] P. Ara, M.A. Moreno, and E. Pardo, Nonstable K-theory for graph algebras, Algebr. Represent. Theory 10 (2007), 157--178.
- Phantom Cuntz-Krieger Algebras.
If A is a C*-algebra, we say that A "looks like a Cuntz-Krieger algebra" if all of the following conditions are satisfied:
- A is unital, purely infinite, nuclear, separable, and has real rank zero.
- A has finitely many ideals.
- Every subquotient of A has finitely generated K0-group, finitely generated and free K1-group, and rank of the K0-group equal to rank of the K1-group.
- The simple subquotients of A are in the bootstrap class of Rosenberg and Schochet.
Question: Do phantom Cuntz-Krieger algebras exist?
Arklint has obtained a number of results concerning phantom Cuntz-Krieger algebras in [Ark13]. She has also shown that simple phantom Cuntz-Krieger algebras do not exist [Ark13, Corollary 3.3], and that phantom Cuntz-Krieger algebras with exactly one ideal do not exist [Ark13, Corollary 3.7].
References
[Ark13] S. Arklint, Do phantom Cuntz-Krieger algebras exist?, preprint.
- The Graded Grothendieck Group as a Classification Tool
Roozbeh Hazrat has outlined problems related to the
graded Grothendieck group and formally conjectured that this group
serves as a complete invariant for the graded isomorphism of Leavitt path
algebras. He has also formulated an analytic version of the conjecture
for graph C*-algebras. More details can be found in this write-up:
Conjectures regarding the Graded Grothendieck Group (and LaTeX source), a write-up by Roozbeh Hazrat
Note: This problem is related to Problem 10 above.
